戻る

ポイント
長さ32の
円順列に、
5桁の2進数が
全て現れる。

実は
一筆書き
と関係!

Press any key ...

解説

定理:
円周上に合計 2ⁿ 個の 0 と 1 を並べる方法で、 0,1 からなる長さ n の任意の文字列が、 その円周上に時計回りに現れるようなものがある。

n=3 の例: 00010111
n=4 の例: 0000111101100101
n=5 の例: 後ろのパタパタの縦の列がそれぞれそうなっている

証明:
次のように グラフ (有向多重グラフ) を作る:

頂点集合 V = { 0,1 からなる長さ n-1 の文字列全て }

辺集合 E = { (x,y) | x,y ∈ V, x の左端の文字を消したものと y の右端の文字を消したものが等しい }

例えば n=4 のとき、 (010,101) や (011,111) や (000,000) は E に属す。
各辺は、長さ n の0/1文字列に対応している。 また、2 辺が有向道となることは、対応する長さ n の文字列たちが求める円順列上で続いて現れることができるということである。
各 x∈V から出る辺、入る辺はそれぞれ偶数本 (2本) ずつあるから、このグラフは一筆書きできる。
一筆書きの各辺 (x,y) を y の右端の文字で置き換えて得られる文字列が、求める円順列となっている。

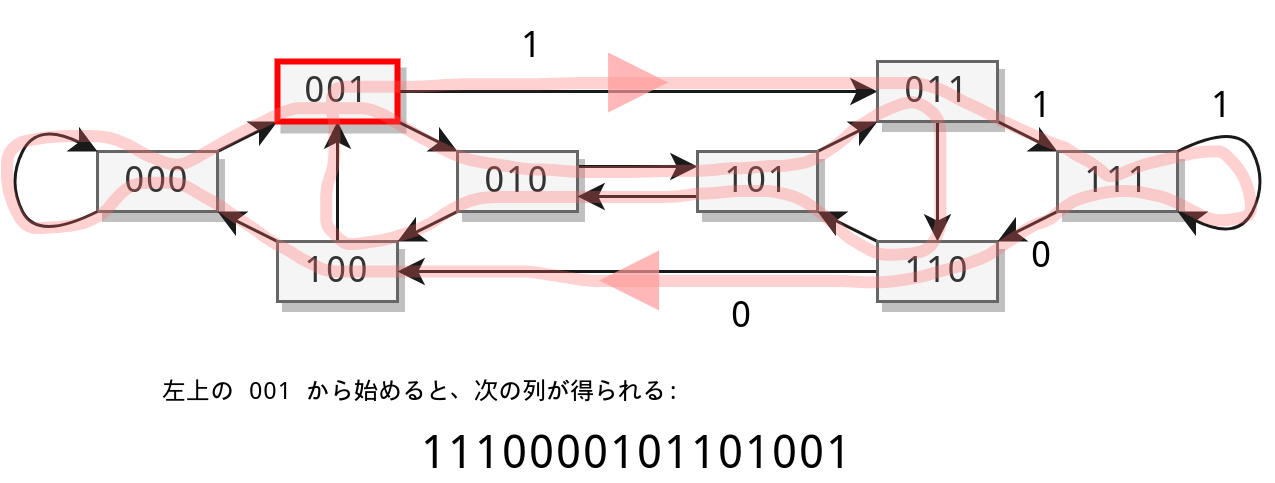
出典: 『離散数学への招待 上』 p.132

minecraft での応用: 2種類のブロックを上記の円順列で並べ、ピストンで循環させることで、5x5 のディスプレイを作れる。(TODO: 動画作成)