雑記 2022/06
0610
「結び目の数学」を読んでいる。
メモ
結び目理論
結び目はもともと理科の分野での発想 (各元素が固有の結び目と対応しているという考え) で、それが長い間純粋数学で研究されていたが、後になって再び自然科学への応用 (DNA分子) が見つかった。
交代結び目
結び目を辿ったとき、交点の通り方が上・下・上・下と交互になっている場合、交代結び目という。
問: どのような結び目の射影図も、いくつかの交点で上下を入れ替えることで、交代結び目にできることを示せ。 (同値でない結び目になってもよい)
証明: ある交点から辿りはじめて、上下交互に交点を通過していく。 最後まで問題なく辿れればOK。 そうでないとすると、ある交点 v で下側を通ったのに、再びその下側を通らなければならない、 という状況になる。 そのような閉歩道 C で最短のものを取る (結び目を多重グラフと見なす)。 始点を v とする。 C で囲まれる領域の外側にある辺を全て削除する (C 上の辺は残す)。
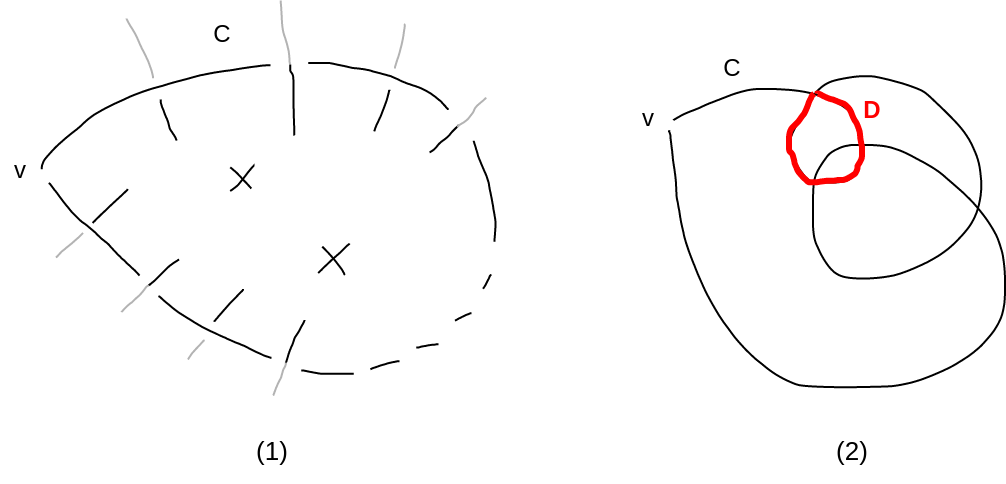
簡単な場合として C が自己交差していないときを考える (図(1))。 v の下を通って C がスタートして、再びその下を通らなければならないことから、 C は偶数本の辺を持つ。
C 上の点は v のみ次数 2 で、その他の点は次数 3 (C 上の辺が 2 本、 C の内側へ向かう辺が 1 本) であり、 C の内側の点は次数 4 である。 よって次数の総和が奇数となるが、これは不可能。
次に C が自己交差する場合を考える (図(2))。 C に含まれる閉歩道で最短のものをとって、 その全ての辺を削除する操作を繰り返す。 このとき、以下の 1 と 2 が言える。 ただしこのような閉歩道は奇数本の辺を持つこと (C の最短性より)、 および一般に 2 つの閉曲線は接している点がなければ偶数個の点で交わることに注意。 議論は慎重さを要する。
- 毎回の操作で、グラフの次数の総和は、偶数だけ減少する。
- 操作が行えなくなったとき C は次数 0 or 2 の点を偶数個、次数 3 の点を奇数個持つ。
よって自己交差がない場合と同様、矛盾が出る。 □
C が8の字の場合?
0614
「整数と平面格子の数学」より
問1: 辺の長さが √5, √17, √18 である三角形の面積を、ピックの定理を用いて求めよ。
3 頂点を (0,0), (-1,2), (3,3) におくとよい。 格子点が境界上に B=5 個、内部には I=3 個あるので、面積は I+(B-2)/2 = 9/2 となる。
ヘロンの公式で確認してみよう (qalc コマンドが便利で、Arch Linux では sudo pacman -S libqalculate でインストールできる)。
$ qalc > s:=(sqrt5+sqrt17+sqrt18)/2 save((sqrt(5) + sqrt(17) + sqrt(18)) / 2, s) ≈ 5.300907145 > sqrt(s(s-sqrt5)(s-sqrt17)(s-sqrt18)) sqrt(s × (s − sqrt(5)) × (s − sqrt(17)) × (s − sqrt(18))) = 9/2 = 4 + 1/2 = 4.5
問2: "格子正三角形" は存在しないことを証明せよ。
証明: ピックの公式より、格子多角形の面積は有理数。 一方、格子多角形の辺の長さは √整数 なので、 辺の長さ a の格子正三角形があれば、 面積は (√3/4)a2 で無理数となる。 □
以上から、辺の長さが全て √整数 という形の三角形に対して、 いつでも問1の方法を使えるわけではないことが分かる。
3 次元空間では格子正三角形がある。
0621
ある騙し絵
問 このだまし絵について説明せよ。

自分の答え
紙の位置を入れ替えただけなのに、 人数が変わっている (1枚目=15人, 2枚目=14人) 。
仕組み
まず上半身のみに注目し、小さい順に番号をつける (赤枠)。
同様に、下半身のみに注目し、小さい順に番号をつける (青枠)。
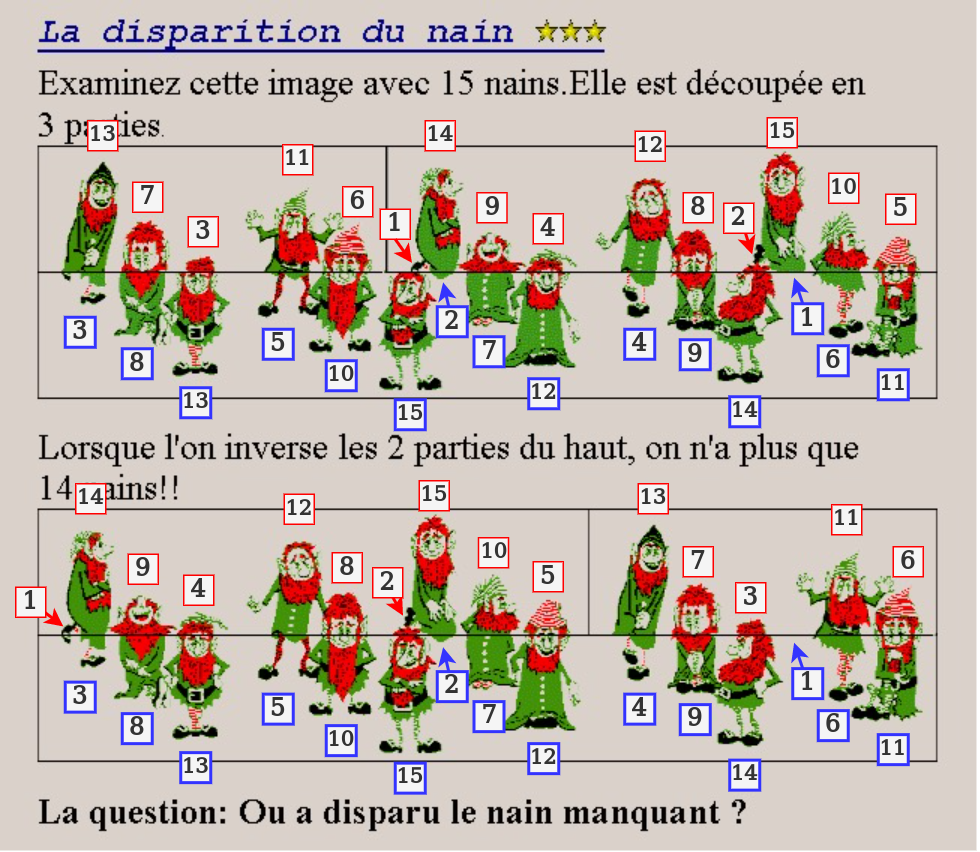
1枚目の絵では、 赤15 と 青1、赤14 と 青2 … のようにペアになっているが、 2枚目の絵では、並び換えの結果、 赤15 と 青2、赤14 と 青3 … のようにペアの和が1ずつ増えている。
そして、青で最も小さいもの (青1) はペア相手がなく、 また赤で最も小さいもの (赤1) はほかのペアに吸収されており、 ここで一人分消滅しているが、 いずれも小さすぎるので不自然ではない。
概念的には、